Генерация профиля NACA в Matlab - Конструкторский

Для дальнейшей разработки программы Aero-PM понадобилась генерация профиля NACA в Matlab. То есть процедура, которая могла бы генерировать координаты четырехзначных профилей NACA с разной хордой и выдавала бы раздельно верхнюю поверхность, нижнюю и среднюю линию. В релиз пока не добавил, но с исходников на GitHub скачать уже можно. Файл NACA4Digit.m.

Генерация профиля NACA 2415 в Matlab. Хорда равна 2. Средняя линия показана желтым цветом. Верхняя поверхность — синим, а нижняя красным.

Генерация профиля NACA: формулы

Вычисления производятся для хорды, равной 1. Результат затем масштабируется. В приведенных формулах, M, P и T(или XX) — это цифры из обозначения профиля NACA MPXX.

Сначала — уравнение средней линии (camber line):

$y_{c}= \begin{cases} \frac{M}{P^{2}}\left[2Px-x^{2}\right] & \text{}\forall x\in\left[0;P\right) \\ \frac{M}{(1-P)^{2}}\left[1-2P+2Px-x^{2}\right] & \text{}\forall x\in\left[P;1\right] \end{cases}$

Координаты по x и y для верхней и нижней поверхности откладываются по нормали от средней линии, поэтому для их вычисления используется производная средней линии по x (градиент):

$\dot{y_{c}}= \begin{cases} \frac{2M}{P^{2}}\left[P-x\right] & \text{}\forall x\in\left[0;P\right) \\ \frac{2M}{(1-P)^{2}}\left[P-x\right] & \text{}\forall x\in\left[P;1\right] \end{cases}$

Затем вычисляются углы при помощи найденных значений производной:

$\Theta=arctg(\dot{y_{c}})$

Теперь — толщина профиля:

$y_{t}=\frac{T}{0.2}\cdot(0.2969\cdot\sqrt{x}-0.1260\cdot x-0.3516\cdot x^2+0.2843\cdot x^3-0.1015\cdot x^4)$

И, наконец — координаты. Обратите внимание, по формулам определяются и координаты x и координаты y точек для обеих поверхностей профиля, верхней и нижней.

$x_{u}=x-y_{t} sin(\Theta)$

$y_{u}=y_{c}+y_{t} cos(\Theta)$

$x_{l}=x+y_{t} sin(\Theta)$

$y_{l}=y_{c}-y_{t} cos(\Theta)$

Затем — масштабирование и график. Для одинаковых масштабов по данным используется daspect([1 1 1]). Иначе профиль получится похожим на шар из-за плохого масштаба по оси y.

Исходный код


function [ xu, xl, yu, yl, yc, x ] = NACA4Digit( m, p, xx, nPanels, c)
% Функция строит 4-х значный профиль NACA по обозначению.
% M, P, XX - цифры из обозначения профиля (MPXX).
chord = 1;
x = 0:chord/nPanels:chord;
nNodes = size(x,2);
% Вычисление средней линии и производной.
yc = zeros(nNodes,1);
dyc = zeros(nNodes,1);
p = (p/10)*chord;
m = (m/100)*chord;
for i=1:nNodes
if 0<=x(i)&&x(i)<p
yc(i) = (m/(p^2))*(2*p*x(i)-x(i)^2);
dyc(i) = (2*m/(p^2))*(p-x(i));
elseif p<=x(i)&&x(i)<=chord
yc(i) = (m/((1-p)^2))*(1-2*p+2*p*x(i)-x(i)^2);
dyc(i) = (2*m/((1-p)^2))*(p-x(i));
end
end
% Вычисление распределения толщины над и под средней линией.
yt = zeros(nNodes,1);
t=xx/100;
for i=1:nNodes
yt(i) = (t/0.2)*(0.2969*sqrt(x(i))-0.1260*x(i)-0.3516*(x(i)^2)+...
0.2843*(x(i)^3)-0.1015*(x(i)^4));
end
% Вычисление координат верхней и нижней линии профиля.
xu = zeros(nNodes,1);
yu = zeros(nNodes,1);
xl = zeros(nNodes,1);
yl = zeros(nNodes,1);
for i=1:nNodes-1
theta = atan(dyc(i));
xu(i) = x(i)-yt(i)*sin(theta);
yu(i) = yc(i)+yt(i)*cos(theta);
xl(i) = x(i)-yt(i)*sin(theta);
yl(i) = yc(i)-yt(i)*cos(theta);
end
xu(nNodes) = chord;
xl(nNodes) = chord;
yu(nNodes) = 0;
yl(nNodes) = 0;
% Масштабирование результатов.
xu = xu*c;
xl = xl*c;
yu = yu*c;
yl = yl*c;
yc = yc*c;
x = x*c;
% Plot.
plot(xu,yu);
hold on;
plot(xl,yl);
plot(x,yc);
daspect([1 1 1])
end

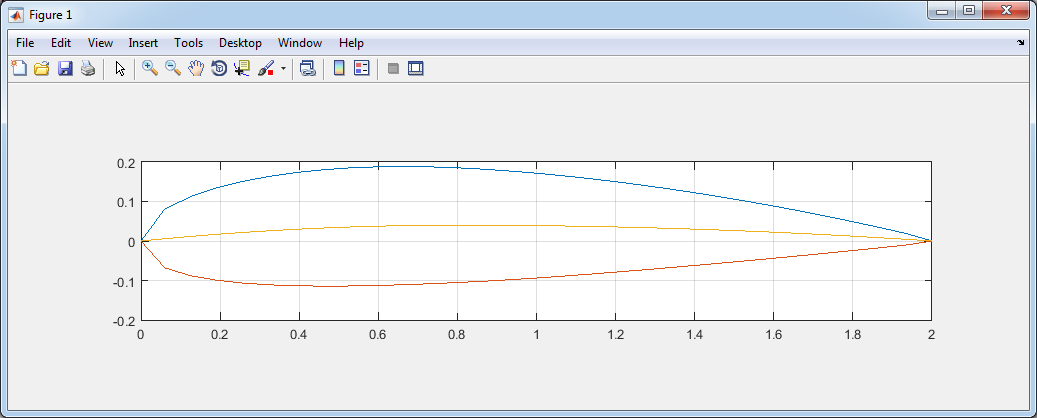
Пример вызова функции NACA4Digit для расчета координат профиля 2415, показанного на рисунке в начале статьи:


[ xu, xl, yu, yl, yc, x ] = NACA4Digit( 2, 4, 15, 30, 2);

Здесь: xu — координаты x для верхней поверхности, xl — координаты x для нижней поверхности, уu — координаты у для верхней поверхности, xu — координаты y для нижней поверхности, yc — средняя линия, которая дается только координатами y и строится по равномерной разбивке хорды x (последний возвращаемый вектор).

На входе: 2, 4, 15 — цифры из обозначения профиля NACA2415. 30 — количество панелей, пока только равномерное. 2 — длина хорды профиля.

Для проверки результатов можно задействовать готовый генератор координат профиля. Например, онлайн генератор четырехзначных профилей NACA.

Генерация профиля NACA: формулы

Исходный код

Добавить комментарий Отменить ответ