Поскольку в статье [2] о реализации метода контрольных объемов теоретическая часть приведена только в виде ссылки на книгу [1], здесь будет перевод небольшого отрывка из этой самой книги. Теория метода контрольных объемов формулируется для некоторого абстрактного свойства ![]() (вместо температуры
(вместо температуры ![]() ).
).
Метод контрольных объемов (1D)
Метод контрольных объемов часто используется при решении задач, связанных с вычислительной гидродинамикой и теплообменом. Рассмотрим одномерный случай установившегося распределения температуры ![]() в теплоизолированном по длине стержне, на концах которого поддерживается постоянная температура.
в теплоизолированном по длине стержне, на концах которого поддерживается постоянная температура.

![]() — площадь поперечного сечения равна 0,001 кв.м,
— площадь поперечного сечения равна 0,001 кв.м, ![]() — коэффициент теплопроводности равен 1000 Вт/мК — это довольно много, коэффициент теплопроводности, например, алюминия равен 210-220 Вт/мК. Буквой P обозначается узел, для которого формируется уравнение, большими буквами W (west) и E (east) обозначаются западный и восточный соседние узлы. Маленькими буквами w и e обозначаются границы контрольного объема с узловой точкой P.
— коэффициент теплопроводности равен 1000 Вт/мК — это довольно много, коэффициент теплопроводности, например, алюминия равен 210-220 Вт/мК. Буквой P обозначается узел, для которого формируется уравнение, большими буквами W (west) и E (east) обозначаются западный и восточный соседние узлы. Маленькими буквами w и e обозначаются границы контрольного объема с узловой точкой P.
Механизация — закрылок
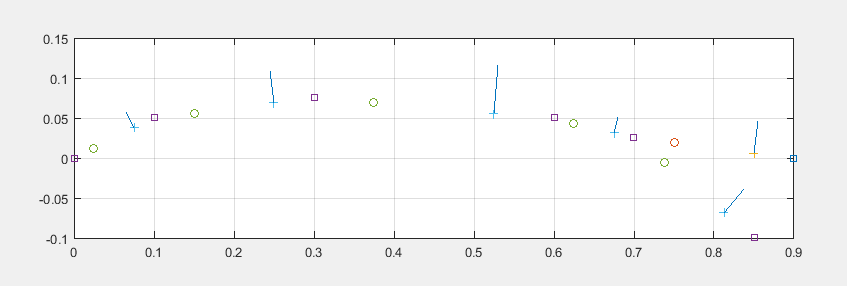
В релизе Aero-PM 0.2.4 поправлена ошибка с минусом. Она хоть и не приводила к неверным результатам, сильно нарушала логику алгоритма. Теперь — все правильно. Рассматривается механизация — закрылок. Обычный отклоняемый закрылок теперь применяется редко, но его проще всего смоделировать. Два расчета: закрылок убран (FlappedFoil_1.txt), закрылок выпущен (FlappedFoil_2.txt). Профиль — без названия (несуществующий).
Обход компонентов сборки в NXOpen
Обход (перечисление) компонентов может понадобиться по разным причинам. Например, для назначения атрибутов компонентам или для чтения каких-то атрибутов. Может быть для составления отчета или перечня. Рассмотрим обход компонентов сборки в NXOpen.
NX Open: установка атрибута
Одним из способов автоматизации работы в Siemens NX является написание программ или журнала при помощи библиотеки NX Open. Часто бывает так: сначала записывается файл журнала, а затем из него убирается все лишнее и оставшийся код копируется в приложение. Можно просто запустить журнал, записанный ранее и ничего не компилировать. Рассмотрим создание атрибута детали в NX.

Точки аэродинамического профиля: формат Selig
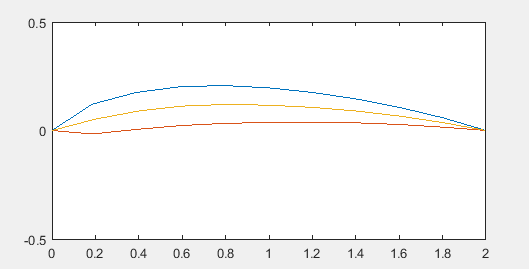
Рассмотрим формирование файла, содержащего точки аэродинамического профиля NACA c четырехзначным номером. Формат Selig.
Читать далее «Точки аэродинамического профиля: формат Selig»
Аэродинамический фокус
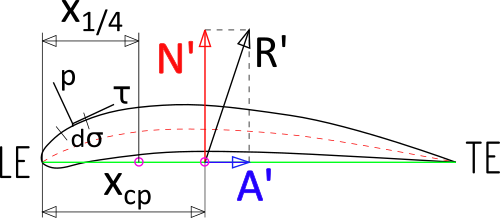
Сделал попытку изучить свойства аэродинамического фокуса при помощи программы Aero-PM. Результаты получились ожидаемые. Сначала рассмотрим, что такое аэродинамический фокус, потом рассмотрим результаты численного эксперимента для профилей NACA 6409 (несимметричный) и NACA 0012 (симметричный). Примеры запуска даны для Aero-PM вер. 0.2.1.
Заметки по NX Часть 2
Заметки по NX Часть 2. Здесь: о поиске компонентов, о том, как удалить дерево построения модели, и как сделать чище содержимое навигатора сборки для экспорта в MS Excel.
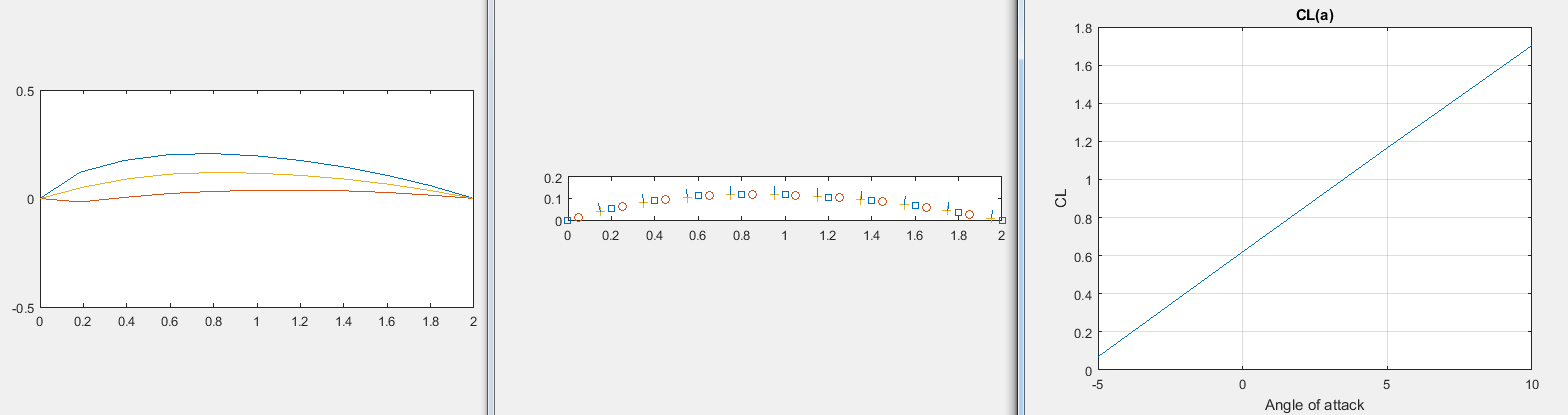
Профиль NACA 6409: Коэффициент подъемной силы
Рассмотрим, какой коэффициент подъемной силы имеет профиль NACA 6409 на углах атаки от -5 до 10 градусов.
Читать далее «Профиль NACA 6409: Коэффициент подъемной силы»
Комплексная скорость и потенциал в Matlab
Программа Aero-PM в настоящее время не имеет средства визуального отображения результатов (только численный вывод в командное окно). Для упрощения отладки, полезно иметь возможность графического отображения линий тока и эквипотенциальных линий. Комплексная скорость и потенциал в Matlab могут быть отображены на двумерных графиках при помощи функций quiver() и contour().

