Рассмотрим бак с водой. В днище бака выполнено отверстие. Задача — рассчитать, как будет выливаться вода из бака, а также проанализировать расчет в Simscape Fluids для применения такого источника жидкости в других схемах. Расчеты по аналитическим формулам для простоты работы с единицами измерения делал в Mathematica. Решение ОДУ расхода и построение графика уровня от времени также выполнено в Mathematica.
Время истечения жидкости — Схема
Схема вот:
Аналитические расчеты
Характеристики бака и аналитические расчеты:
— диаметр отверстия в баке, 
— площадь отверстия, 
— площадь основания бака (бак с прямыми стенками, например — вертикальный цилиндр), 
— высота уровня воды в баке в начале процесса, 
— ускорение свободного падения, 
— плотность воды, 
— кинематическая вязкость.
— скорость потока через отверстие, вычисляется по формуле Торричелли. В англоязычной литературе, эта формула называется законом Торричелли. Расход 
— это просто скорость потока , умноженная на площадь отверстия . UnitConvert преобразует единицы расхода в л/мин. Время вытекания воды из бака составило по аналитическим расчетам 1016.8 секунды.
Время истечения жидкости — Модель Simscape Fluids
Теперь, результаты моделирования:
Результат похож на ожидания. На первом графике отображается объем воды в баке. Первоначальный объем равен 125 л, согласно геометрии бака и высоте уровня. По истечении почти 1000 секунд времени, бак опустошится 
. Расход остается ненулевым даже при нулевом объеме ввиду специфики математической модели бака. На верхнем графике можно заметить даже отрицательный объем. Стоит учитывать это обстоятельство при моделировании более сложных схем. Начальный же расход вполне точно соответствует полученному при аналитическом расчете.
Коэффициент Pipeline pressure loss coefficient принимается для бака равным единице. Также следует внимательнее относиться к установке начальных значений переменным. На рисунке ниже показана настройка блока Бак. В расчетах за начальную переменную принимается исходный уровень, а не объем. Показаны соответствующие настройки приоритета начальных значений, в данном случае, объем 20 л игнорируется (поэтому крестик). При установке равного приоритета обоим начальным значениям переменных, результаты моделирования данной схемы будут неточными.
Аналитическое уравнение
Решение аналитического уравнения.
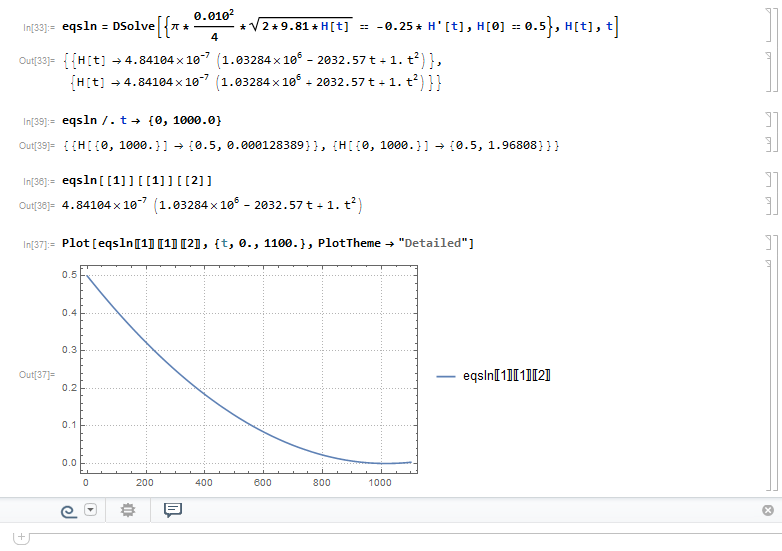
Как видно из рисунка, дифференциальное уравнение представляет собой равенство, в левой части которого расход, полученный при помощи уравнения Торричелли, а в правой части — расход по своему определению. По идее, расход это 
, но так как стенки бака прямые, площадь мы выносим за производную. Таким образом, уравнение имеет вид:
Его решение показано синей линией на графике уровня от времени. График уровня проходит минимум при 
.