Программа Aero-PM в настоящее время не имеет средства визуального отображения результатов (только численный вывод в командное окно). Для упрощения отладки, полезно иметь возможность графического отображения линий тока и эквипотенциальных линий. Комплексная скорость и потенциал в Matlab могут быть отображены на двумерных графиках при помощи функций quiver() и contour().
Комплексная скорость и потенциал в Matlab: типы течений
Будут рассмотрены четыре типа течений: однородный поток, угловой поток, источник и дублет. Комплексная скорость обозначена w, комплексный потенциал обозначен W.
1 Однородный поток

Matlab:
wf = @(z)z./z; WF = @(z)z; CVelocityPlot2D( -2-2i, 2+2i, wf, WF, 10, 100);

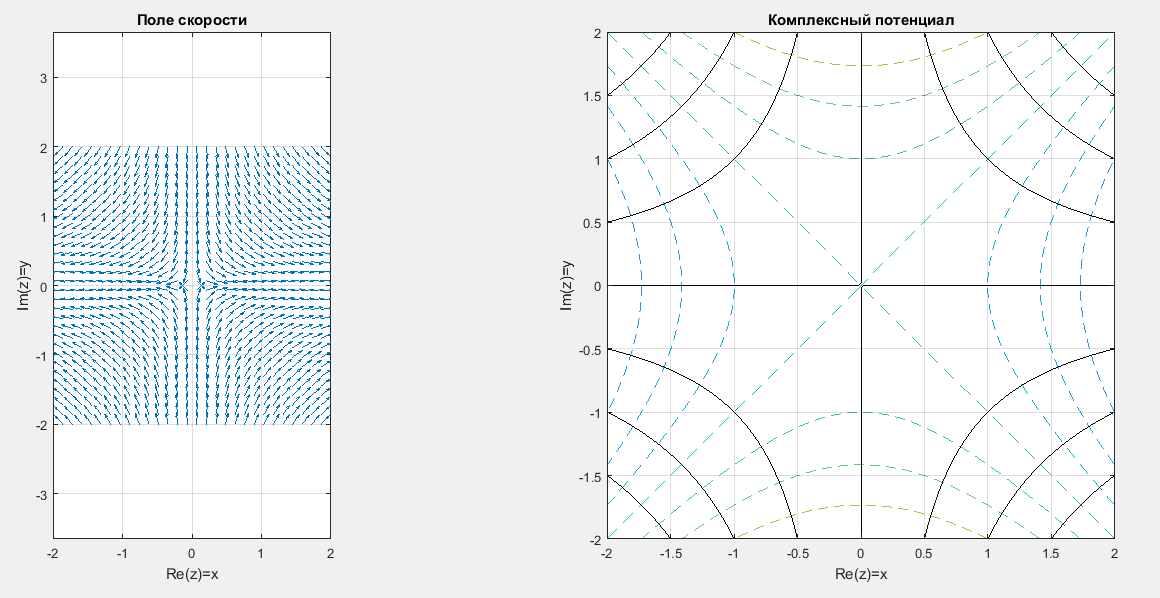
2 Угловой поток

Matlab:
wf = @(z)z; WF = @(z)(-z.^2)./2; CVelocityPlot2D( -2-2i, 2+2i, wf, WF, 30, 100);
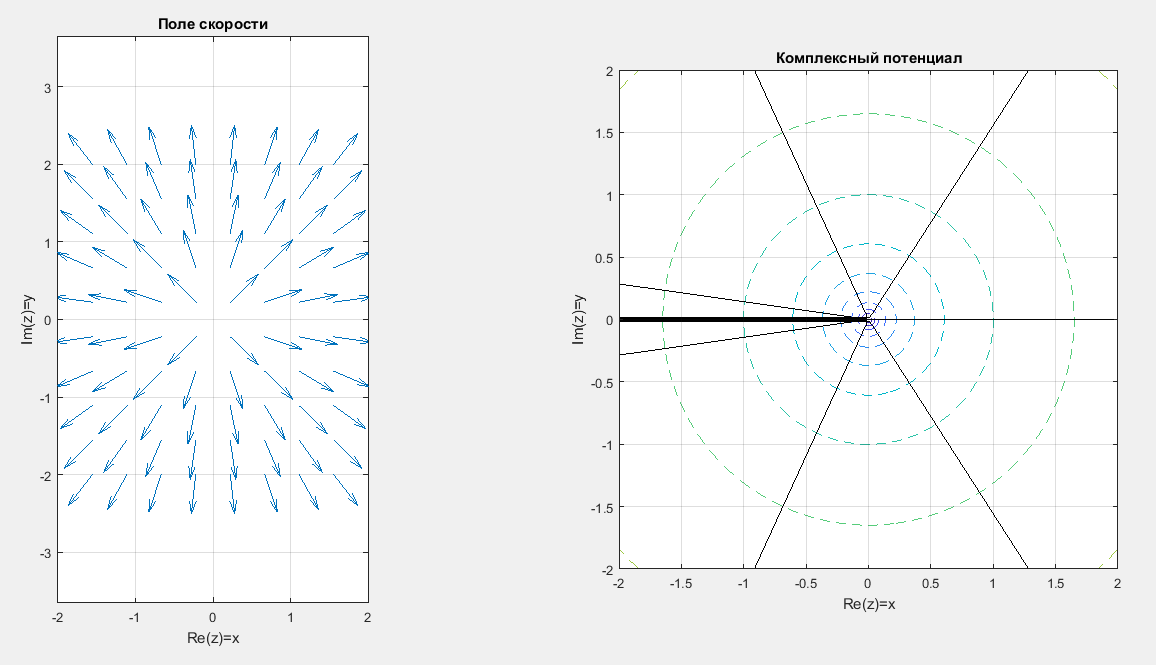
3 Источник

Matlab:
wf = @(z)1./z; WF = @(z)log(.z); CVelocityPlot2D( -2-2i, 2+2i, wf, WF, 10, 100);
4 Дублет

Matlab:
wf = @(z)z.^-2; WF = @(z)-z.^-1; CVelocityPlot2D( -2-2i, 2+2i, wf, WF, 10, 100);

Исходный текст
McBain — Theory of Lift — Introductory Computational Aerodynamics with MATLAB (стр.49-55). В книге функции печати скорости и потенциала разделены.
function CVelocityPlot2D( ll, ur, wf, WF, nodesNumwf, nodesNumWF )
% McBain - Theory of Lift - Introductory Computational
% Aerodynamics with MATLAB (стр.49-55)
% Пример вызова:
% wf = @(z)(abs(z)>1).*(1-z.^-2);
% WF = @(z)(abs(z)>1).*(z + 1./z);
% CVelocityPlot2D( -2-2i, 2+2i, wf, WF, 10, 100);
% Подготовка 2D данных для комплексной скорости.
xwf = linspace (real(ll), real(ur), nodesNumwf);
ywf = linspace (imag(ll), imag(ur), nodesNumwf);
[Xwf, Ywf] = meshgrid(xwf, ywf);
Zwf = complex(Xwf, Ywf);
wwf = wf(Zwf);
% Масштаб стрелок.
scaledwf = wwf ./ abs(wwf);
% Подготовка 2D данных для комплексного потенциала.
xWF = linspace (real(ll), real(ur), nodesNumWF);
yWF = linspace (imag(ll), imag(ur), nodesNumWF);
[XWF, YWF] = meshgrid(xWF, yWF);
ZWF = complex(XWF, YWF);
% Печать двух графиков.
f = figure(1);
figure(f);
% Линии тока (комплексной скорости).
subplot(1,2,1)
quiver(real(Zwf), imag(Zwf), real(scaledwf), -imag(scaledwf))
axis([real(ll), real(ur), imag(ll), imag(ur)],'on', 'equal')
box on
grid on
xlabel('Re(z)=x');
ylabel('Im(z)=y');
title('Поле скорости');
% Изопотенциальные линии.
subplot(1,2,2)
contour (real(ZWF), imag(ZWF), real(WF(ZWF)), '--')
hold on
contour (real(ZWF), imag(ZWF), imag(WF(ZWF)), 'k-')
axis ([real(ll), real(ur), imag(ll), imag(ur)],'on', 'equal')
box on
grid on
xlabel('Re(z)=x');
ylabel('Im(z)=y');
title('Комплексный потенциал');
hold off
end

