Аэродинамический фокус - Конструкторский

Сделал попытку изучить свойства аэродинамического фокуса при помощи программы Aero-PM. Результаты получились ожидаемые. Сначала рассмотрим, что такое аэродинамический фокус, потом рассмотрим результаты численного эксперимента для профилей NACA 6409 (несимметричный) и NACA 0012 (симметричный). Примеры запуска даны для Aero-PM вер. 0.2.1.

Аэродинамический фокус. Обозначения — Обозначения: N’ — погонная нормальная сила (на единицу длины), A’ — погонная осевая сила, R’ — погонная полная аэродинамическая сила, p и τ — напряжения нормальное и касательное, LE — Leading Edge (передняя кромка), TE — Trailing Edge (задняя кромка). Красным пунктиром показана средняя линия, зеленым цветом — хорда. Начало координат совпадает с передней кромкой (LE), X1/4 — координата фокуса (1/4 хорды), Xcp — координата центра давления.

Общие сведения

При обтекании тела газом или жидкостью, на это тело действует распределенная по всей площади аэродинамическая нагрузка. Как обычно делается в физике для решения практических задач, вся эта нагрузка приводится к силе, называемой полной аэродинамической силой $R$ . Решить нужно две проблемы. Во-первых, нужна величина силы, а во-вторых, нужно её прикладывать в правильной точке тела. Рассмотрим эти две задачи по порядку.

Напряжения

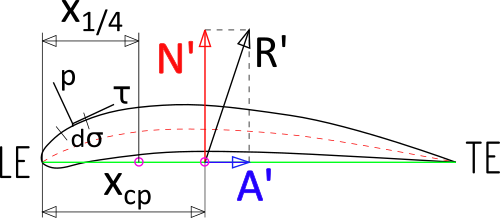
Для решения первой проблемы с величиной силы, введем понятие напряжения. Рассмотрим малый элемент поверхности $\Delta \sigma$ (dσ на двумерном рисунке). Напряжением называется предел отношения аэродинамической силы, действующей на выделенный элемент поверхности к площади этого элемента поверхности:

$\vec{p}=\lim_{\Delta \sigma \rightarrow 0} \frac{\Delta P}{\Delta \sigma}$

Это векторная величина, направленная в сторону вектора полной аэродинамической силы, действующей на элемент поверхности $\Delta \sigma$ .

У выделенного элемента поверхности dσ (см. рисунок) есть нормаль и касательные. Не вдаваясь в детали, будем называть нормальным напряжением $p$ проекцию полного напряжения на нормаль, а касательным напряжением $\tau$ — проекцию полного напряжения на вектор какой-то касательной к элементу поверхности. Если жидкость покоится, то она оказывает воздействие на стенки (например сосуда) только в виде нормального напряжения. Касательная составляющая появляется при движении жидкости. То есть для покоящейся жидкости, имеем $\vec{p}=p \cdot \vec{n}$ . И скалярная величина $p$ называется гидростатическим давлением, оно не зависит от ориентации площадки [1, стр.16-17].

Величины аэродинамической силы и момента: интегральные формулы

Итак, есть нормальные и касательные напряжения. Их названия даже закреплены стандартом ГОСТ 23281-78 [см. 5]. Если проинтегрировать напряжения по всей поверхности тела, получится величина полной аэродинамической силы $R$ , если же проинтегрировать напряжения, домноженные на расстояние от элемента поверхности до некоторой точки (например, носок профиля), то получится величина аэродинамического момента. Формулы, применительно к профилю, выглядят так [2, стр.19]:

$\begin{cases} & N'=-\int_{LE}^{TE} (p_{u}cos\theta + \tau_{u}sin\theta)ds_{u} + \int_{LE}^{TE} (p_{l}cos\theta - \tau_{l}sin\theta)ds_{l} \text{ } \\ & A'=\int_{LE}^{TE} (-p_{u}sin\theta + \tau_{u}cos\theta)ds_{u} + \int_{LE}^{TE} (p_{l}sin\theta + \tau_{l}cos\theta)ds_{l} \text{ } \\ & M'_{LE}= \int_{LE}^{TE} [(p_{u}cos\theta + \tau_{u}sin\theta)x-(p_{u}sin\theta - \tau_{u}cos\theta)y]ds_{u}+ \text{} \\ & + \int_{LE}^{TE} [(-p_{l}cos\theta + \tau_{l}sin\theta)x+(p_{l}sin\theta + \tau_{l}cos\theta)y]ds_{l}\text{ } \end{cases}$

$'$ — величина на единицу размаха, удельная сила или момент,
$N'$ и $A'$ — нормальная и аксиальная(проекция на хорду профиля) составляющие полной аэродинамической силы $R'$ .
$M'_{LE}$ — аэродинамический момент относительно передней кромки профиля.
$LE$ и $TE$ — Leading Edge и Trailing Edge. Передняя и задняя кромки — пределы интегрирования.
$p_{u}, p_{l}$ — нормальное напряжение на верхней (upper) и нижней (lower) поверхностях профиля.
$\tau_{u}, \tau_{l}$ — касательное напряжение на верхней и нижней поверхностях профиля.
$\theta$ — угол наклона выделенного элемента поверхности.
$ds_{u}, ds_{l}$ — малый элемент поверхности.

Нам не нужно сейчас что-то вычислять по этим формулам. Важно вот что: величина полной аэродинамической силы (в компонентах $N'$ и $A'$ ) и величина момента $M'_{LE}$ вычисляются по одним и тем же исходным данным, т.е. по нормальным и касательным напряжениям $p$ и $\tau$ . В формулу момента входят дополнительно координаты $x$ и $y$ , выполняющие роль плеча нагрузки на элемент поверхности.

При малых углах атаки, нормальная сила $N$ — почти то же самое, что подъёмная $Y$ . Нормальная перпендикулярна хорде (связанная система координат), а подъёмная — скорости набегающего потока (скоростная система координат). См.[7].

Точка приложения аэродинамической силы

Осталось определиться с точкой приложения полученной аэродинамической силы. Как раз для этого мы определяли момент $M'_{LE}$ от распределенной нагрузки относительно заданной точки (выбрана передняя кромка — leading edge).

Момент сосредоточенной силы — это сила, умноженная на плечо. Эффект от полной аэродинамической силы должен быть таким же, как от распределенной нагрузки. Значит, момент $M'_{LE}$ , полученный по интегральной формуле должен быть равен моменту сосредоточенной силы. Условимся считать, что точка приложения лежит на хорде, поэтому момент от осевой составляющей $A'$ не учитываем. Рассматриваем только момент от нормальной силы $N'$ . Итак, момент у нас есть и сила есть. Прикладывать вектор силы $N'$ нужно на таком плече, чтобы при этом, момент её соответствовал величине момента, полученного по указанной ранее формуле. $M'_{LE}$ это момент относительно носка профиля, значит сосредоточенную силу надо прикладывать в точке с таким плечом $x_{cp}$ от носка, которое даст требуемую величину момента. $M'_{LE}=-(x_{cp}) N'$ , значит $x_{cp}=-M_{LE}/N'$ . Точка приложения аэродинамической силы, выбираемая таким образом называется центром давления (center of pressure) [2, стр.28].

Очевидно, что если бы мы записали формулу для момента $M'$ относительно какой-то другой точки, вместо передней кромки (LE), то полную аэродинамическую силу пришлось бы размещать, ориентируясь на расстояние от другой точки. А вот например, что если бы мы перед интегрированием, выбрав точку угадали бы так, что попали бы в центр давления? Тогда получившийся при интегрировании момент был бы равен нулю. С этим выводом связано одно из определений центра давления: это точка, относительно которой аэродинамический момент равен нулю.

Итак, если мы размещаем силу в центре давления, то момент не прикладываем и эффект от приложенной силы будет эквивалентным эффекту распределенной нагрузки. Если разместим силу в точке передней кромки, то мы должны приложить момент $M'_{LE}$ в этой же точке, тогда эффект от приложенной силы тоже будет эквивалентным распределенной нагрузке. Получается, что можно разместить силу в любой точке профиля, отличной от центра давления, если имеется значение момента наподобие $M'_{LE}$ для приложения в этой же точке. Ниже показаны эквивалентные схемы нагружения. Сверху — распределенная, в середине — нагрузка в центре давления (без момента), снизу — в точке передней кромки, с моментом $M'_{LE}$ .

Различные способы приложения нагрузки, эквивалентной распределенной.

Аэродинамический фокус профиля

При изменении угла атаки профиля или скорости полета, распределение напряжений $p$ и $\tau$ меняется, и центр давления смещается. Это делает неудобным его применение в расчетах. Например, при $N'\rightarrow 0$ , мы получаем $x_{cp}\rightarrow \infty$ .

В теоретической аэродинамике есть теория тонкого профиля [3 — стр.177, 2 — стр. 298, 6 стр.]. В соответствии с этой теорией, коэффициент момента относительно точки, расположенной на 1/4 хорды от носка, вычисляется следующим образом [2, стр. 310]:

$c_{m,c/4}=\frac{\pi}{4}(A_{2}-A{1})$

Обратите внимание на то, что в этой формуле нет зависимости от угла атаки. В формулах для вычисления коэффициентов $A_{2}$ и $A_{1}$ такой зависимости тоже нет. Это означает, что коэффициент момента, а значит и сам аэродинамический момент относительно этой точки постоянны при любых углах атаки. Точку с таким свойством называют аэродинамическим фокусом (aerodynamic center a.c.). В справочной литературе позиция фокуса (a.c. position) дается двумя относительными координатами $x/c$ и $y/c$ [4, стр.131-151].

В рамках теории тонкого профиля, фокус, независимо от его формы находится на 1/4 хорды [6, стр.135].

Известно, что подъемная сила и положение центра давления изменяются при изменении угла атаки, т.к. изменяется подъемная сила (см. выражение для $x_{cp}$ ). Допустим, что угол атаки увеличился. При этом подъемная сила увеличилась, то есть на тело стала действовать дополнительная распределенная нагрузка, которая может быть приведена к сосредоточенной силе. Вертикальная составляющая у этой силы есть и должна быть куда-то приложена. Поскольку общий момент относительно аэродинамического фокуса не меняется при изменении угла атаки, считают, что дополнительная результирующая сосредоточенная сила — приращение подъемной силы от изменения угла атаки прикладывается в точке фокуса. Так её плечо равно нулю. То есть аэродинамический фокус принимают за точку приложения прироста подъемной силы.

Расчет в Aero-PM

Запуск в Matlab:

[ xu, xl, yu, yl, yc, x ] = NACA4Digit( 6, 4, 09, 100, 2);
Run_BatchMode(2, [-5 0 5 10]', 1.225, 'tmpFoil.txt');

Вывод на экран:

Аэродинамический фокус. Расчет NACA 6409 в Aero-PM. На левом графике — зависимость коэффициента подъемной силы от угла атаки, на среднем — зависимость момента относительно передней кромки от угла атаки, на правом графике — зависимость момента относительно фокуса от угла атаки.

Момент относительно 1/4 хорды меняется незначительно при изменении угла атаки от 1.46 до 1.55. Это соответствует ожиданиям при рассмотрении момента относительно аэродинамического фокуса несимметричного профиля NACA 6409.

Момент относительно фокуса для симметричного профиля при изменении угла атаки равен нулю, а не константе. Например, рассмотрим профиль NACA 0012:

[ xu, xl, yu, yl, yc, x ] = NACA4Digit( 0, 0, 12, 100, 2);
Run_BatchMode(2, [-5 0 5 10]', 1.225, 'tmpFoil.txt')

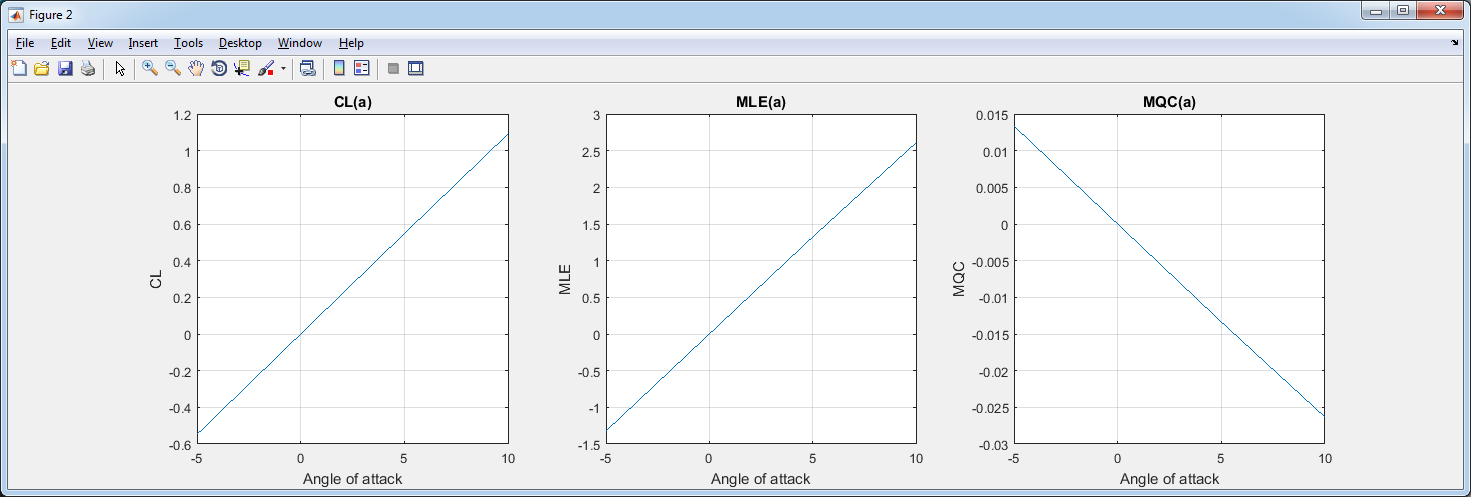
Аэродинамический фокус. Расчет NACA 0012 в Aero-PM.

Значения момента относительно 1/4 хорды (фокуса) на правом графике очень небольшие. Характерно для симметричного профиля.

Литература

А.М. Мхитарян — Аэродинамика, 1976
John D. Anderson — Fundamentals of Aerodynamics, 3-rd ed. 2001
Н.С. Аржаников, В.Н. Мальцев — Аэродинамика, 1956
I.H. Abbott, A.E. von Doenhoff, L.S. Stivens, Jr. — Summary of Airfoil Data, 1945
ГОСТ 23281-78 — Аэродинамика летательных аппаратов. Термины, определения и буквенные обозначения.
Н.С. Аржаников, Г.С. Садекова — Аэродинамика летательных аппаратов, 1983
ГОСТ 20058-80 — Динамика летательных аппаратов в атмосфере. Термины, определения и обозначения.