Граничные условия в МКО (1D) - Конструкторский

Граничные условия в МКО: дополнительные пояснения к реализации МКО описанной в статье [2]. В этой статье приводится перевод Раздела 4.3 книги [1] с примером 4.1 по теплопередаче. Раздел 4.1 и 4.2 — см. [3]. Необходимость этих дополнительных пояснений обусловлена тем, что в статьях по теории и по реализации нет явных указаний на принцип обработки граничных условий.

Граничные условия в МКО: основные сведения

В одномерной реализации метода контрольных объемов, есть три типа уравнений: уравнения для внутренних узлов, уравнение (одно) для граничного левого узла и ещё уравнение (одно) для граничного правого узла. Для этих уравнений общим является необходимость подсчетов коэффициентов $a$ .

Начало перевода [1] стр. 118.

4.3 Рабочие примеры: одномерный установившийся процесс диффузии

В этом разделе представлено приложение метода конечных объемов для решения задачи переноса тепла. Уравнение, характеризующее этот процесс имеет вид:

$\frac{\text{d}}{\text{d}x}\left(k \frac{\text{d}T}{\text{d}x}\right)+S=0$ (4.12)

Здесь $k$ — это коэффициент теплопроводности, он занимает место $\Gamma$ из уравнения (4.3). В роли зависимой переменной $\phi$ , выступает температура $T$ . Источниковый член может представлять, к примеру, тепловыделение вследствие протекания в стержне электрического тока. Обработка граничных условий и источниковых составляющих будет рассмотрена на рабочих примерах далее.

Пример 4.1

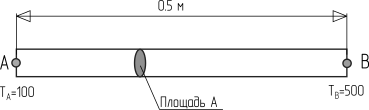
Рассмотрим задачу теплопереноса без источников в изолированном стержне, на концах которого поддерживается постоянная температура 100ºК и 500ºК. Эта одномерная задача изображена на рис. 4.3.

Уравнение процесса имеет вид:

$\frac{\text{d}}{\text{d}x}\left(k \frac{\text{d}T}{\text{d}x}\right)=0$ (4.13)

Необходимо определить распределение температуры в стержне при установившемся процессе теплопередачи. Коэффициент теплопроводности $k=1000$ Вт/(м·К), площадь поперечного сечения стержня $A=10e-3$ кв.м.

Граничные условия МКО - Пример 4.3 Рисунок 4.3 — Рис. 4.3 Граничные условия в МКО — Пример 4.3

Разделим стержень по длине на пять равных контрольных объемов, как показано на рис. 4.4. В этом случае, размер ячейки будет равен $\delta x=0.1$ м.

Граничные условия в МКО - Сетка Рисунок 4.4 — Рис. 4.4 Граничные условия в МКО — Сетка

Сетка состоит из пяти узлов. Для каждого из узлов 2,3 и 4 температура в соседних узлах равна некоторым неизвестным узловым величинам. Следовательно, дискретные уравнения по форме (4.10) возможно представить для каждого внутреннего контрольного объема таким образом:

$\left(\frac{k_{e}}{\delta x_{PE}}A_{e} + \frac{k_{w}}{\delta x_{WP}}A_{w} \right)T_{P} = \left(\frac{k_{w}}{\delta x_{WP}}A_{w}\right) T_{W} + \left(\frac{k_{e}}{\delta x_{PE}}A_{e}\right) T_{E}$ (4.14)

Будем считать, что теплопроводность $k_{e}=k_{w}=k$ и площадь сечения стержня $A=A_{w}=A_{e}$ постоянны по длине. Также постоянным считаем шаг сетки $\delta x$ . Индексы у этих величин далее мы опускаем.

$a_{P} T_{P} = a_{W} T_{W} + a_{E} T_{E}$ (4.15)

Здесь $a_{W}=\frac{k}{\delta x} A$ , $a_{E}=\frac{k}{\delta x} A$ , $a_{P} = a_{W}+a_{E}$ . Слагаемые $S_{u}$ и $S_{p}$ из (4.11) здесь равны нулю, так как по условию задачи, в (4.13) отсутствуют источники.

Узлы 1 и 5 в нашей задаче являются граничными. Их обсуждением мы сейчас займемся. Интегрирование уравнения (4.13) по контрольному объему, расположенному вокруг точки 1 дает следующее:

$k A\left( \frac{T_{E}-T_{P}}{\delta x}\right) -k A\left( \frac{T_{P}-T_{A}}{\delta x/2}\right) =0$ (4.16)

Это уравнение демонстрирует нам то что поток сквозь границу A контрольного объема аппроксимируется в предположении, что распределение температуры между точками A (на границе) и P (узел внутри объема) выбрано линейным. Уравнение (4.16) возможно привести к следующему виду:

$\left(\frac{k}{\delta x}A + \frac{2 k}{\delta x}A \right)T_{P} = 0\cdot T_{W} + \left(\frac{k}{\delta x}A\right) T_{E} + \left(\frac{2 k}{\delta x}A\right) T_{A}$ (4.17)

Сравнивая уравнение (4.17) с (4.10), легко видеть, что фиксированное граничное условие (заданная температура) вводится в дискретную модель в виде источникового члена $(S_{u}+S_{p}T_{p})$ , где $S_{u}=(2kA/\delta x)T_{A}$ и $S_{u}=-2kA/\delta x$ . Кроме того, связь с западной гранью теперь подавлена путем установки $a_{w}=0$ .

Теперь, уравнение (4.17) может быть записано в стандартном виде, как например, было записано (4.11). Это уравнение и будет дискретным уравнением для узла 1, на левой границе расчетной области:

$a_{P}T_{P}=a_{W}T_{W}+a_{E}T_{E}+S_{u}$ (4.18)

Здесь $a_{W}=0$ , $a_{E}=kA/\delta x$ , $a_{P}=a_{W}+a_{E}-S_{p}$ , $S_{p}=-2kA/\delta x$ , $S_{u}=2kAT_{A}/\delta x$ .

Таким же образом можно рассмотреть пятый узел, находящейся на другой границе расчетной области. Его дискретное уравнение имеет вид:

$k A\left( \frac{T_{B}-T_{P}}{\delta x/2}\right) -k A\left( \frac{T_{P}-T_{W}}{\delta x}\right) =0$ (4.19)

Как и прежде, для аппроксимации теплового потока сквозь границу контрольного объема, мы подразумеваем линейное распределение температуры между узлом P и граничной точкой B. Уравнение (4.19) может быть переписано в виде:

$\left(\frac{k}{\delta x}A + \frac{2 k}{\delta x}A \right)T_{P} = \left(\frac{k}{\delta x}A\right) T_{W} + 0\cdot T_{E} + \left(\frac{2 k}{\delta x}A\right) T_{B}$ (4.20)

Дискретное уравнение для узла 5 выглядит так:

$a_{P}T_{P}=a_{W}T_{W}+a_{E}T_{E}+S_{u}$ (4.21)

Здесь $a_{W}=kA/\delta x$ , $a_{E}=0$ , $a_{P}=a_{W}+a_{E}-S_{p}$ , $S_{p}=-2kA/\delta x$ , $S_{u}=2kAT_{A}/\delta x$ .

Итак, процесс дискретизации привел нас к двум дополнительным уравнениям для граничных узлов 1 и 5. Теперь для каждого узла есть уравнение. Подстановка численных исходных данных дает $kA/\delta x=100$ и далее легко определяются коэффициенты каждого дискретного уравнения. Результирующий набор уравнений имеет вид:

$\begin{pmatrix} 300T_{1}=100T_{2}+200T_{A}\\ 200T_{2}=100T_{1}+100T_{3}\\ 200T_{3}=100T_{2}+100T_{4}\\ 200T_{4}=100T_{3}+100T_{5}\\ 300T_{5}=100T_{4}+200T_{B} \end{pmatrix}$ (4.22)

Результирующий набор уравнений запишем так:

$\begin{pmatrix} 300 & -100 & 0 & 0 & 0 \\ -100 & 200 & -100 & 0 & 0 \\ 0 & -100 & 200 & -100 & 0 \\ 0 & 0 & -100 & 200 & -100 \\ 0 & 0 & 0 & -100 & 300 \end{pmatrix} \cdot \begin{pmatrix} T_{1} \\ T_{2} \\ T_{3} \\ T_{4} \\ T_{5} \end{pmatrix} = \begin{pmatrix} 200T_{A} \\ 0 \\ 0 \\ 0 \\ 200T_{B} \end{pmatrix}$ (4.23)

Решив систему (4.23) мы получим искомые значения температуры в узлах. Для несложных задач, когда число узлов небольшое, систему легко ввести вручную и решить в Matlab. Для $T_{A}=100$ и $T_B}=500$ решением (4.23) будет вектор:

$\begin{pmatrix} T_{1} \\ T_{2}\\ T_{3}\\ T_{4}\\ T_{5} \end{pmatrix}=\begin{pmatrix} 140 \\ 220 \\ 300 \\ 380 \\ 460 \end{pmatrix}$ (4.24)

Точным решением является линейное распределение температуры между граничными точками по закону $T=800x+100$ .

Конец перевода [1] стр. 121.

Литература

[1] — H.K. Versteeg, W. Malalasekera — An Introduction to Computational Fluid Dynamics. The Finite Volume Method (2-nd ed)

[2] — Реализация МКО 1D.

[3] — Теория 1D для общего свойства $\phi$ .

Граничные условия в МКО: основные сведения

4.3 Рабочие примеры: одномерный установившийся процесс диффузии

Пример 4.1

Литература

Добавить комментарий Отменить ответ